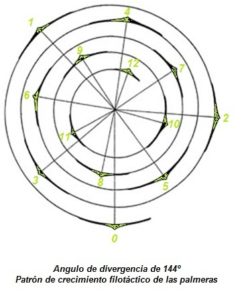
FILOTAXIS EN PALMERAS
Las Palmeras por regla general solo tienen un punto de crecimiento, el meristema apical, que es el encargado de producir las hojas. Con el tiempo van saliendo hojas nuevas en posición vertical, que van desplazando hacia la base de la corona las más viejas, de modo que partiendo del centro de la misma, vamos encontrando hojas jóvenes, adultas, maduras y finalmente hojas muertas. Normalmente las palmeras tienden a mantener un número de hojas estable, siempre y cuando no se rompa su equilibrio natural por cualquier circunstancia como una poda eliminando hojas verdes (B. Moya, J. Plumed, C. Littardi 2005).
Inicialmente cuando la palmera nace de la semilla, sus hojas tienen una disposición dística, es decir que se insertan sobre el tallo, a lo largo de dos líneas opuestas. Esta disposición persiste hasta la edad adulta en pocas especies, como Oenocarpus distichus, Orania disticha y Wallicha disticha, pero en la gran mayoría, la disposición de las hojas se convierte en helicoidal, es decir, que las hojas están esparcidas sobre el tallo, ordenadas generalmente sobre una espiral que se llama “Espiral generatriz”(John Dransfield, Natalie W. Uhl, Conny B. Asmussen, William J. Baker, M. M. Harley and C. E. Lewis 2008).
Podemos pensar que la disposición de las hojas en el tronco es algo casual, pero realmente no es así, en la naturaleza muchas plantas siguen unos patrones matemáticos, para poder aprovechar al máximo el espacio y optimizar su exposición al sol, la lluvia, etc. A medida que el tronco se desarrolla, se producen hojas espaciadas regularmente. A pesar de esto, normalmente las hojas no crecen directamente una sobre la otra, ya que si no, las de arriba no dejarían a las de debajo, obtener la luz del sol necesaria. Para que esto no suceda, el paso de una hoja a la siguiente está caracterizado por un desplazamiento o crecimiento giratorio alrededor del tronco.
Si tomamos una hoja determinada de un tallo y contamos el numero de hojas consecutivas hasta encontrar otra hoja con la misma orientación, este número es, por regla general, un término de la sucesión de Fibonacci (Pisa, s.XII-XIII), y si mientras contamos dichas hojas vamos girando el tronco de la planta, en sentido contrario a la agujas del reloj, y contamos el numero de vueltas que debemos dar a dicho tronco hasta llegar a la siguiente hoja con la misma orientación, resulta ser también un término de la sucesión de Fibonacci.
Se trata de una sucesión de números muy simple, en la que cada término, es la suma de los dos anteriores.
Sucesión de Fibonacci
Los números de Fibonacci poseen varias propiedades interesantes. Quizás una de las más curiosas, es que el cociente de dos números consecutivos de la serie se aproxima a la denominada “Proporción áurea”. Este número descubierto por los renacentistas, tiene un valor de (1 + raíz de 5) /2 = 1,61803…, y se le denomina con la letra griega Phí.
No haremos una introducción detallada de la historia de esta sucesión ni de su descubridor, pero si es interesante destacar las innumerables y sorprendentes propiedades que posee y en la cantidad de procesos y construcciones naturales en los que aparece. En la mayoría de especies vegetales la cantidad de hojas necesarias para dar un giro completo al tallo sigue la secuencia de Fibonacci. En las flores podemos ver la misma sucesión, ya que la mayoría de ellas, poseen 2,3,5,8,13,21,34,51,89 pétalos, y en el corazón de las mismas, podemos ver espirales cuyo número en ambos sentidos se corresponden a dicha sucesión.
FACTOR FILOTACTICO
Llamamos factor filotáctico asociado a una palmera, al cociente m/n, entre el número “m” que sería el número de hojas que habrían al dar una vuelta completa al tronco en un sentido, y “n” el número de hojas que nos encontraríamos en el sentido contrario.
Ej: nº de hojas hacia la derecha “5” y numero de hojas hacia la izquierda “8”, así el valor filotáctico de esa planta sería 5/8, 5 y 8 son números de la sucesión de Fibonacci.
ESTUDIO EN CAMPO
|
Individuo
|
Especie
|
Nº Hojas
|
Vueltas
|
Diámetro
|
Altura
|
|
1
|
Phoenix canariensis
|
8/13
|
1
|
1,95
|
4m
|
|
2
|
Phoenix canariensis
|
13/21
|
1
|
2,70
|
10m
|
|
3
|
Phoenix canariensis
|
13/21
|
1
|
2,45
|
6m
|
|
Individuo
|
Especie
|
Nº Hojas
|
Vueltas
|
Diámetro
|
Altura
|
|
1
|
Phoenix dactylifera
|
5/8
|
1
|
–
|
15m
|
|
2
|
Phoenix dactylifera
|
5/8
|
1
|
–
|
15m
|
|
3
|
Phoenix dactylifera
|
8/13
|
1
|
1,40
|
8m
|
|
4
|
Phoenix dactylifera
|
8/13
|
1
|
1,60
|
2m
|
|
5
|
Phoenix dactylifera
|
8/8
|
1
|
1,35
|
6m
|
|
6
|
Phoenix dactylifera
|
5/8
|
1
|
–
|
4m
|
|
7
|
Phoenix dactylifera
|
8/13
|
1
|
–
|
12m
|
En un estudio hecho por el autor a diferentes ejemplares de las especies Phoenix dactylifera y Phoenix canariensis, se ha comprobado que la mayoría de ellas cumplen con un patrón filotáctico en el que se observan espirales en dos sentidos, una de ellas corre de izquierda a derecha en la cual hay 5 o 8 hojas en la P. dactylifera y 8 o 13 en la P. canariensis, que están en la misma línea de sucesión hasta dar una vuelta completa al tronco, y otra de derecha a izquierda con 8 o 13 hojas y 13 o 21 hojas respectivamente, en la misma línea de sucesión. Se ha observado que alguno de los ejemplares estudiados no cumplen con esta norma y siguen unos patrones distintos.
EL ANGULO DE DIVERGENCIA
La reunión de patrones filotácticos en algunos vegetales genera la siguiente serie, en función del ángulo entre los puntos de inserción de las hojas contiguas: 180º, 120º, 144º, 135º, 138º…
Esta serie converge hacia 137º 30’ 28”, ángulo que divide el círculo en su sección áurea, llamado el ángulo de oro. Siguiendo este patrón de crecimiento filotáctico, las palmeras y demás plantas hacen que las hojas a lo largo del tronco crezcan en posiciones que optimicen su exposición al sol.